Introduction to stat in R: Cheatsheet

A cheatsheet to find your way around your stats

Rémy Beugnon

Last updated on 2022-08-04 11 min read tutorial, stat

Content

Introduction

Check your data
Build your hypothesis
Build your model
Check your model fit. Are the statistical assumptions met?
No, data transformation and corrections
Yes, extract your results

Useful links and tutorials

Introduction

The slides of this lecture can be find here

Stepwise analyses

Check your data
Build your hypothesis
Build your model
Check your model fit. Are the statistical assumptions met?
No, data transformation and corrections
Yes, extract your results

1. Check your data

1.1. Load your data

How to load your data in “df”:

.csv file

df = read.csv(file = 'name-of-your-file.csv')

.txt file

df = read.delim(file = 'name-of-your-file.txt')

.xlsx file (Excel files also with xls)

library(readxl)

df = read_xlsx(path = 'name-of-your-file.xlsx', sheet = 'name of the sheet')

1.2. Your dataset structure

Look at your dataframe:

View(df)

Explore the structure:

str(df)

## 'data.frame':    180 obs. of  6 variables:
##  $ TSP          : chr  "1-E34" "10-G17" "100-Q21" "101-Q21" ...
##  $ C.loss_Mi1   : num  88.3 56.9 86.8 59.4 59.1 ...
##  $ N.loss_Mi1   : num  96 55 84.1 58.7 68.3 ...
##  $ lit.rich     : int  1 1 2 1 1 2 1 1 2 2 ...
##  $ neigh.sp.rich: int  1 1 2 2 2 2 3 1 2 2 ...
##  $ fall         : num  74 21.8 72 38.2 66.1 ...

1.3. Your data structure

1.3.1. Plot all the variables

plot(df)

1.3.2. Plot the variables’ distribution

Example with C loss during decomposition (“C.loss_Mi1”)

boxplot(df$C.loss_Mi1)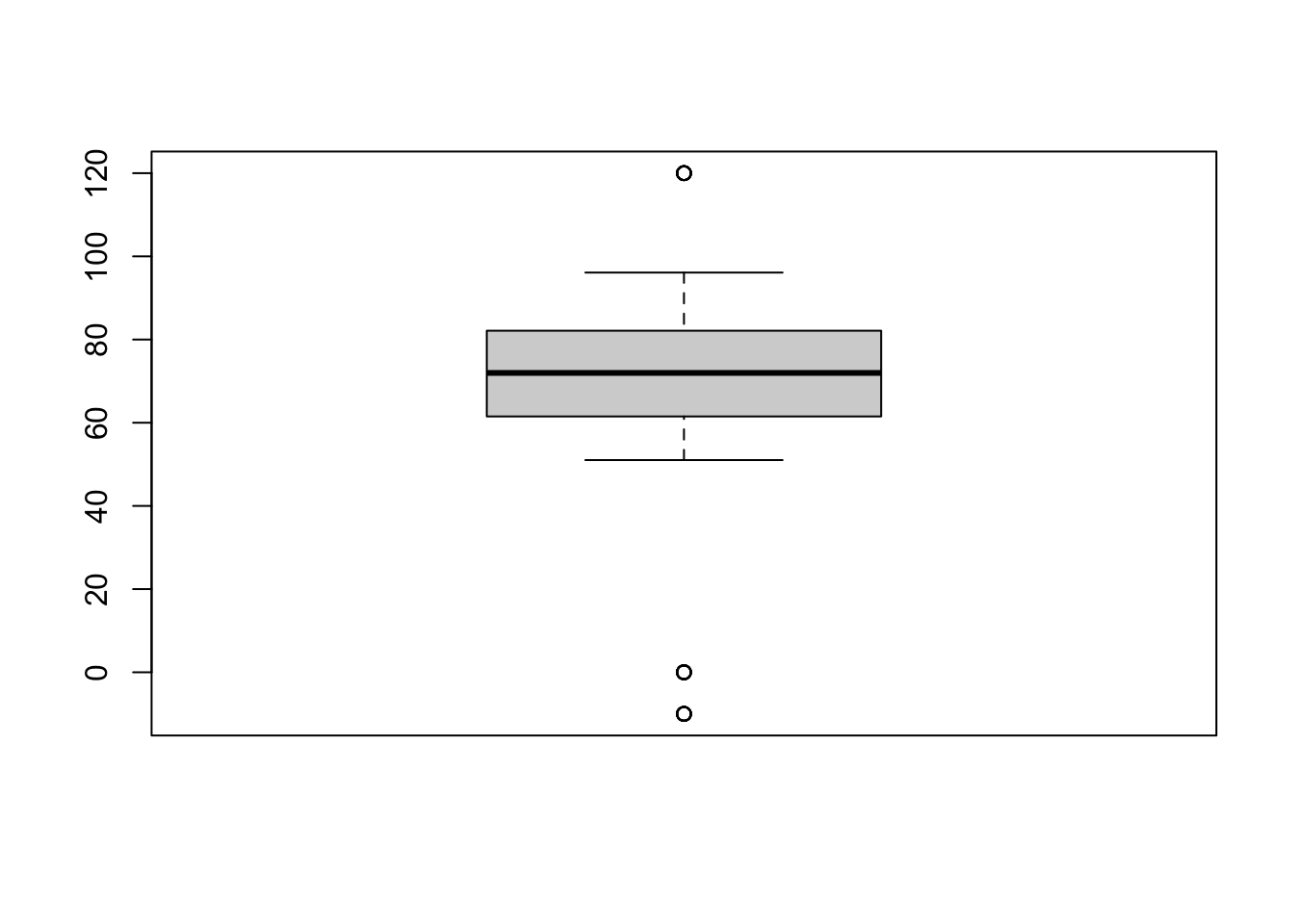

ggplot2 version

library(ggplot2)

ggplot(data = df, aes(y = C.loss_Mi1, x = " ")) + # structure of the graph
  geom_boxplot() +                                # add the boxplot
  geom_jitter() +                                 # show the points distribution 
  labs(x = '', y = "C loss [%]") +                # add labels to the axis
  theme_classic()                                 # make it pretty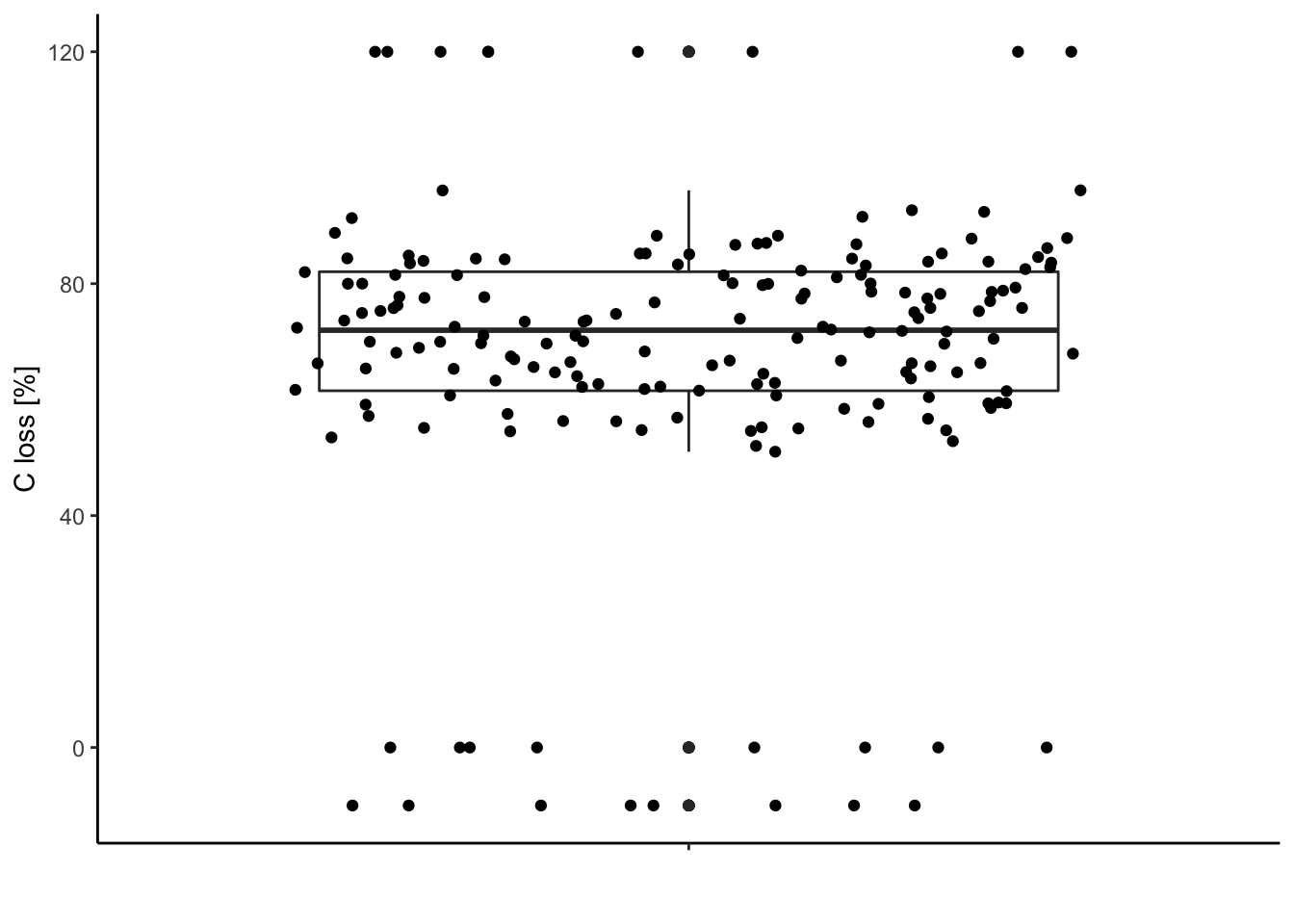

1.3.3. Compare this distribution to the possible range of data

The carbon loss (%) during litter decomposition should be above 0% (intact leaves) and below 100% (completely decomposed).

Check for data out of the range (possible typos, mistakes during measurements …).

Visually:

ggplot(data = df, aes(y = C.loss_Mi1, x = " ")) + # structure of the graph
  geom_boxplot() +                                # add the boxplot
  geom_jitter() +                                 # show the points distribution 
  labs(x = '', y = "C loss [%]") +                # add labels to the axis
  theme_classic() +                               # make it pretty
  geom_hline(yintercept = 0) +                    # add line at 0%
  geom_hline(yintercept = 100)                    # add line at 100%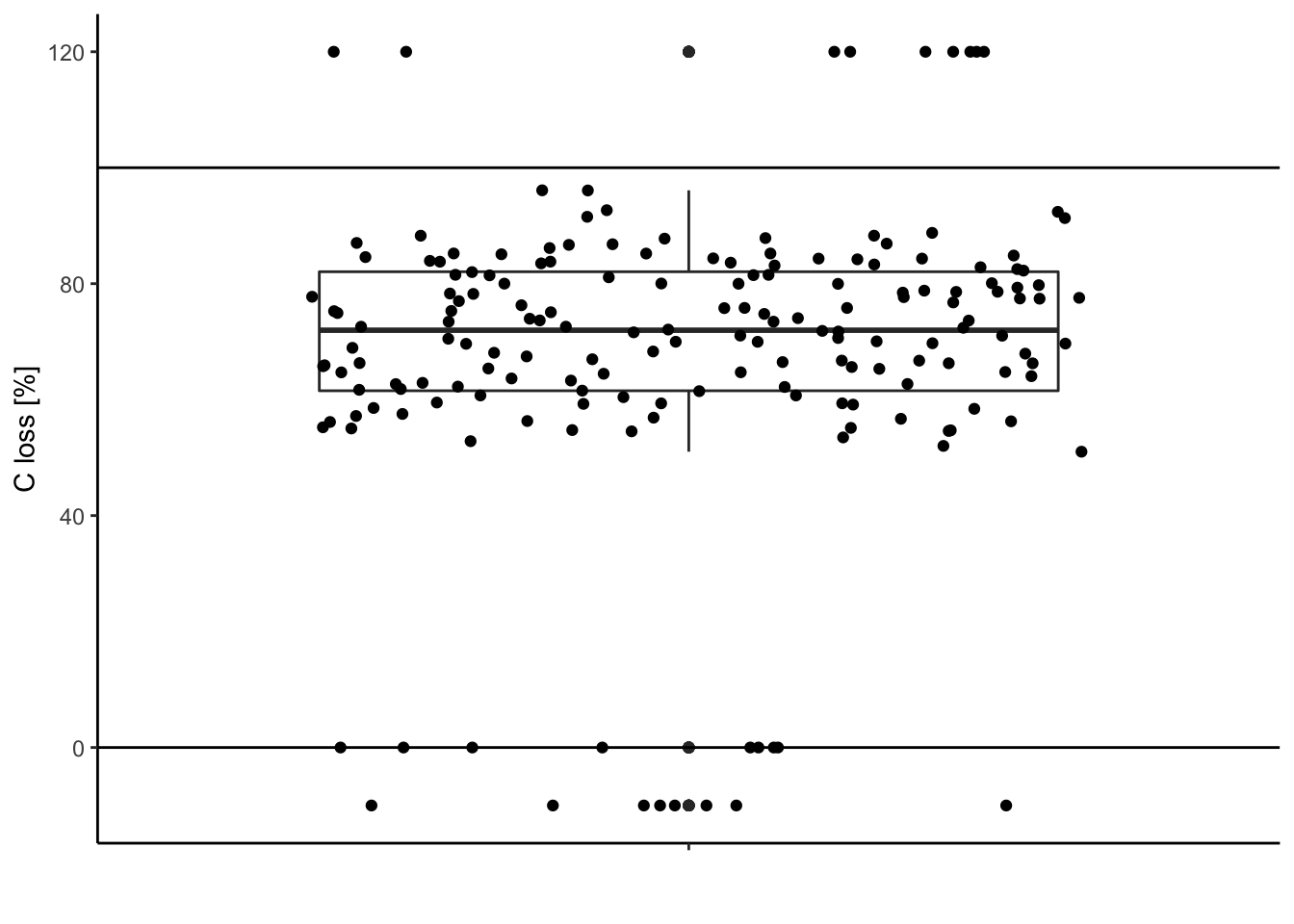

Extract these outliers:

df[df$C.loss_Mi1 < 0 | df$C.loss_Mi1 > 100,] # | means "OR"

##          TSP C.loss_Mi1 N.loss_Mi1 lit.rich neigh.sp.rich fall
## 156 outliers        120        120        1            12    1
## 157 outliers        120        120        1            12    1
## 158 outliers        120        120        1            12    1
## 159 outliers        120        120        1            12    1
## 160 outliers        120        120        1            12    1
## 161 outliers        120        120        1            12    1
## 162 outliers        120        120        1            12    1
## 163 outliers        120        120        1            12    1
## 164 outliers        120        120        1            12    1
## 173 outliers        -10        -10       50            50 1000
## 174 outliers        -10        -10       50            50 1000
## 175 outliers        -10        -10       -1             3 1000
## 176 outliers        -10        -10       -1             3 1000
## 177 outliers        -10        -10       -1             3 1000
## 178 outliers        -10        -10       -1             3 1000
## 179 outliers        -10        -10       -1             3 1000
## 180 outliers        -10        -10       -1             3 1000

With dplyr:

library(dplyr)

df %>%
  filter(C.loss_Mi1 < 0 | C.loss_Mi1 > 100) # filter your rows under conditions

##         TSP C.loss_Mi1 N.loss_Mi1 lit.rich neigh.sp.rich fall
## 1  outliers        120        120        1            12    1
## 2  outliers        120        120        1            12    1
## 3  outliers        120        120        1            12    1
## 4  outliers        120        120        1            12    1
## 5  outliers        120        120        1            12    1
## 6  outliers        120        120        1            12    1
## 7  outliers        120        120        1            12    1
## 8  outliers        120        120        1            12    1
## 9  outliers        120        120        1            12    1
## 10 outliers        -10        -10       50            50 1000
## 11 outliers        -10        -10       50            50 1000
## 12 outliers        -10        -10       -1             3 1000
## 13 outliers        -10        -10       -1             3 1000
## 14 outliers        -10        -10       -1             3 1000
## 15 outliers        -10        -10       -1             3 1000
## 16 outliers        -10        -10       -1             3 1000
## 17 outliers        -10        -10       -1             3 1000

1.3.4. Clean your dataset

You can inverse the condition and save the selected rows in df. Be careful, this will overwrite your data frame (in R), it is always wise to have a save copy.

df.save = df # save the data before cleaning in df.save

df = 
  df %>%
  filter(!(C.loss_Mi1 < 0 | C.loss_Mi1 > 100)) # "!" inverse the conditions

Alternatives:

df = 
  df %>%
  filter(C.loss_Mi1 >= 0 & C.loss_Mi1 <= 100)        # "&" both conditions needed

df = df[df$C.loss_Mi1 >= 0 & df$C.loss_Mi1 <= 100, ] # in base R

Data after cleaning:

ggplot(data = df, aes(y = C.loss_Mi1, x = " ")) + # structure of the graph
  geom_boxplot() +                                # add the boxplot
  geom_jitter() +                                 # show the points distribution 
  labs(x = '', y = "C loss [%]") +                # add labels to the axis
  theme_classic() +                               # make it pretty
  geom_hline(yintercept = 0) +                    # add line at 0%
  geom_hline(yintercept = 100)                    # add line at 100%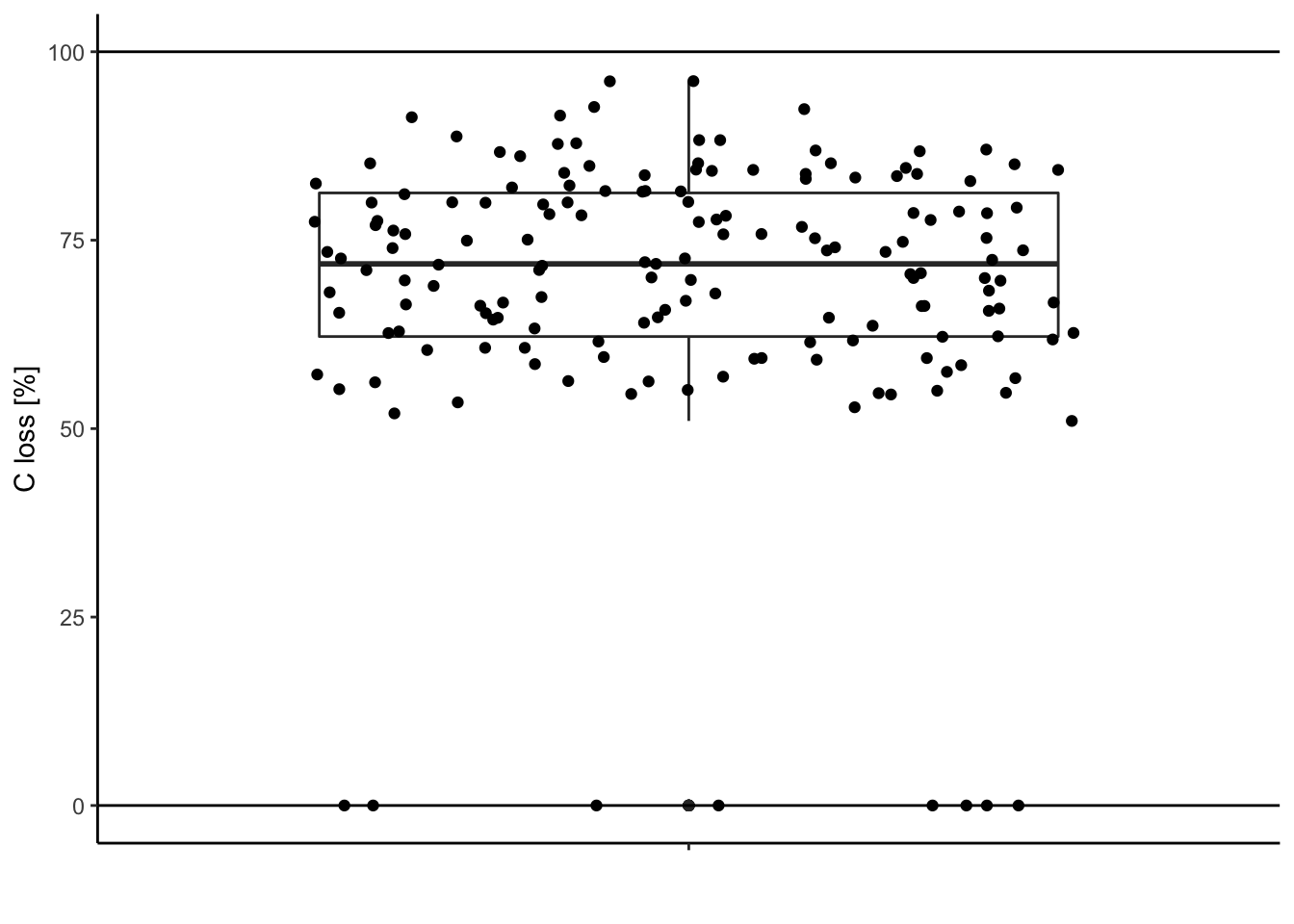

Looks better, no?!

2. Build your hypotheses

2.1. Hypotheses

This as nothing to do with R. In our case:

We expect carbon loss (C.loss_Mi1) to increase with litter species richness (lit.rich).

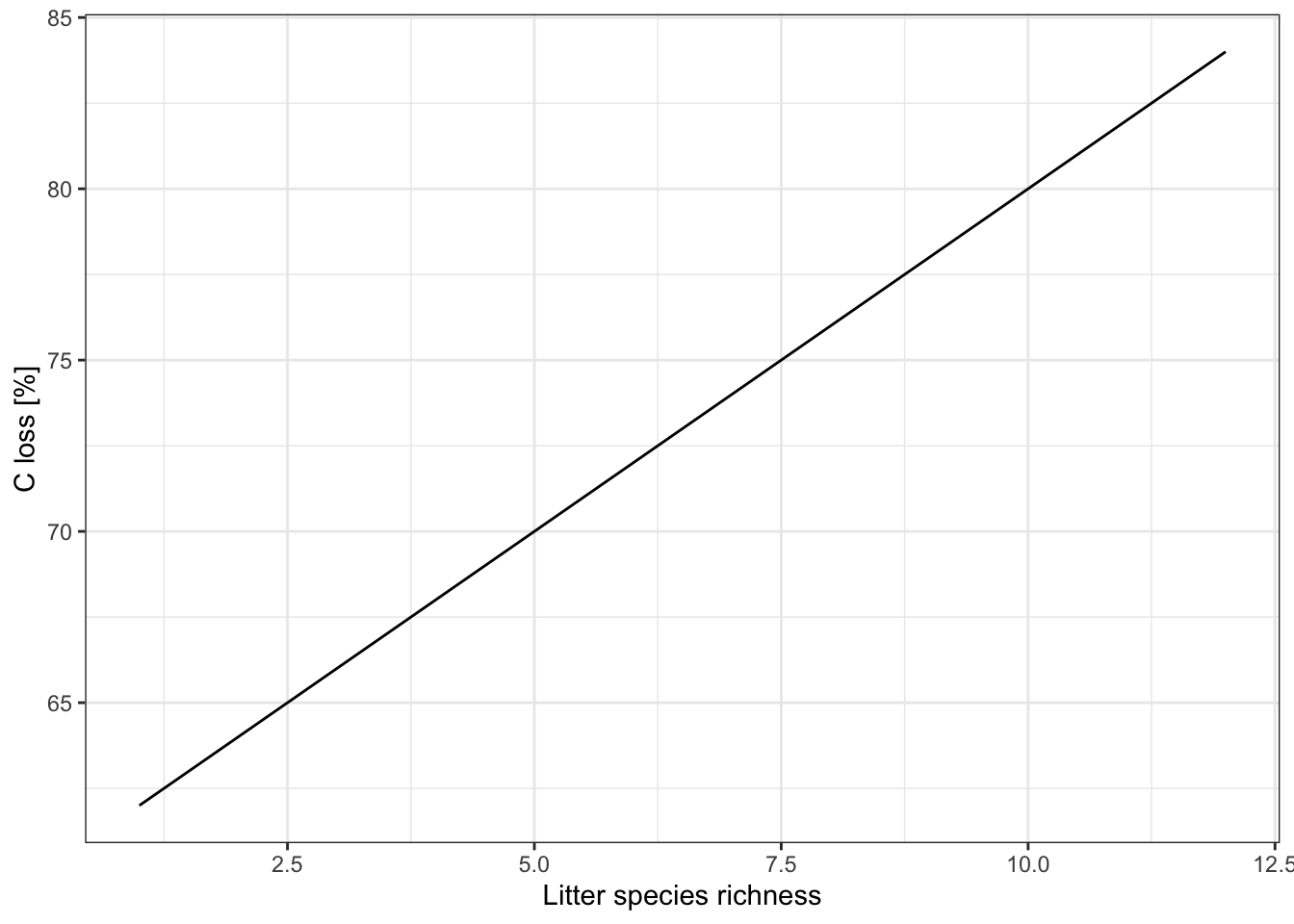
2.2. distribution

What is the expected distribution of the response variable C.loss?

In short:

Distribution	Sampling	Example
Normal	Continuous measurements	size, flux, biomass …
Poisson	Discrete counting	number of species, number of individuals
Binomial	Yes/No	presence-absence of species
Beta	Percentages	decomposition rate
…

N.B. the beta distribution takes into account the bounding between 0 and 1 (or 0 and 100). In our case where our variable values are far from these limits, the normal distribution can also be used and will give similar results.

3. Build your model

3.1. Identify the parameters of your model

Response variable: C.loss_Mi1

Explanatory variable: lit.rich

Formula: C.loss_Mi1 ~ lit.rich

Relation type: linear

Data frame: df

Distribution of the residuals: Normal

3.2. Fit your model on your data

mod = lm(data = df, formula = 'C.loss_Mi1 ~ lit.rich') # the lm function fit linear model with Normal distribution assumption on the residuals

Other residual distribution type:

Poisson distribution

mod = glm(data = df, formula = 'y ~ x', family = poisson())

Binomial distribution

mod = glm(data = df, formula = 'y ~ x', family = binomial())

4. Check your model fit. Are the statistical assumption met?

New in town: the “performance” package

4.1. Model fit

library(performance)

check_model(mod)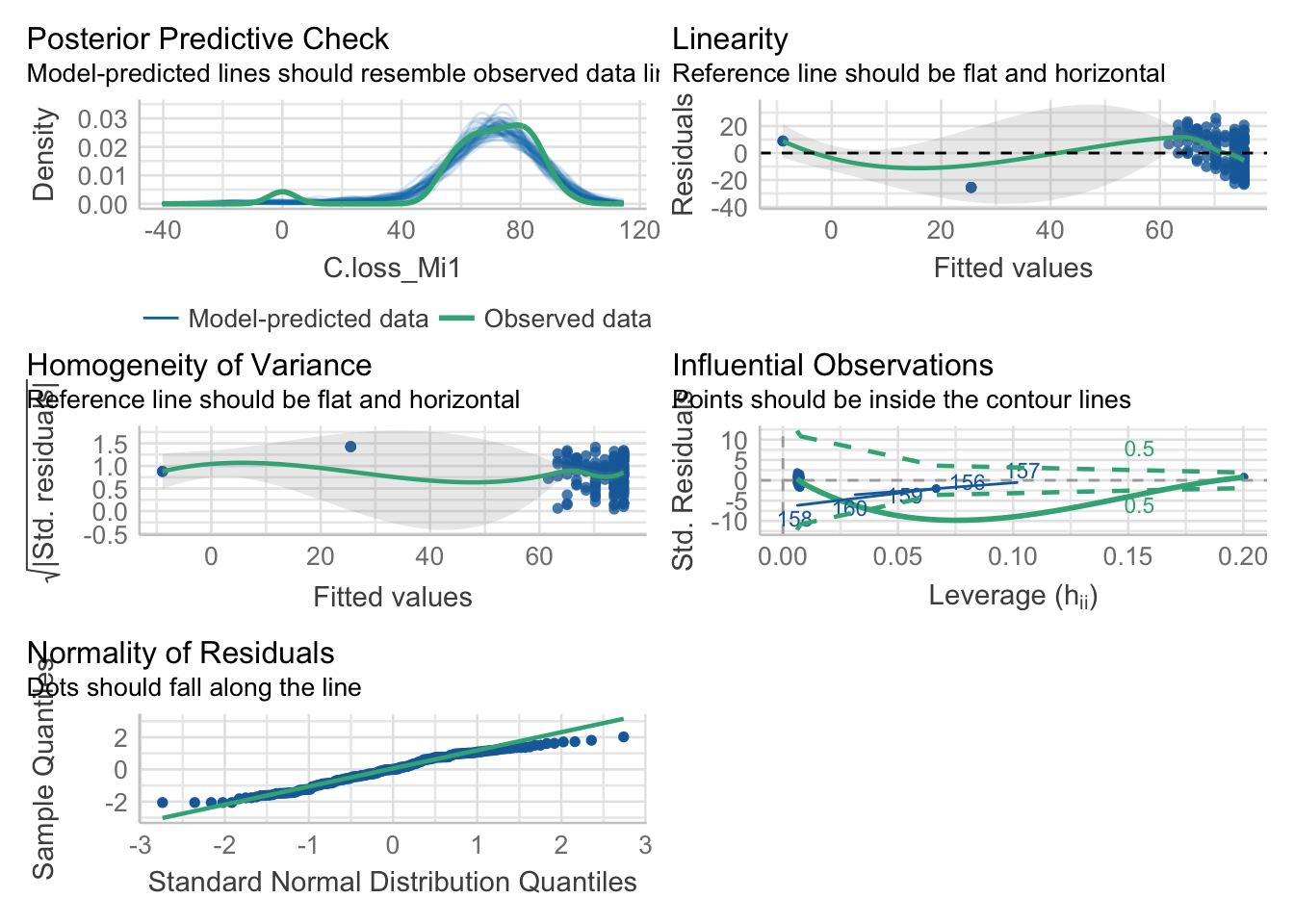

4.2. Check outliers

check_outliers(mod)

## OK: No outliers detected.

4.3. Check possible distribution of residuals

check_distribution(mod)

## # Distribution of Model Family
## 
## Predicted Distribution of Residuals
## 
##  Distribution Probability
##        normal         66%
##       tweedie         22%
##       weibull          6%
## 
## Predicted Distribution of Response
## 
##                Distribution Probability
##                     tweedie         59%
##  neg. binomial (zero-infl.)          9%
##                      normal          9%

4.4. Check normality of the residuals

check_normality(mod)

## Warning: Non-normality of residuals detected (p = 0.002).

4.5. Check heteroscedasticity of variance

check_heteroscedasticity(mod)

## Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.021).

Remember that these tests are often really conservative. They are useful to make your choices but need to be considered having in mind the sample size and data structure.

Here, our model doesn’t seem to meet the assumption of heteroscedasticity and normality of the residuals.

5. No, data transformation and corrections

5.1. Check your data (again)

Look for surprising values, they could be typos.

ggplot(data = df, aes(y = C.loss_Mi1, x = " ")) + # structure of the graph
  geom_rect(data = NULL,                          # add rectangle to show outliers
            aes(ymin = -5, ymax = 5, 
                xmin = -Inf, xmax = Inf), 
            alpha = .005, fill = 'red', color = NA) +
  geom_boxplot() +                                # add the boxplot
  geom_jitter() +                                 # show the points distribution 
  labs(x = '', y = "C loss [%]") +                # add labels to the axis
  theme_classic() +                               # make it pretty
  geom_hline(yintercept = 0) +                    # add line at 0%
  geom_hline(yintercept = 100)                  # add line at 100%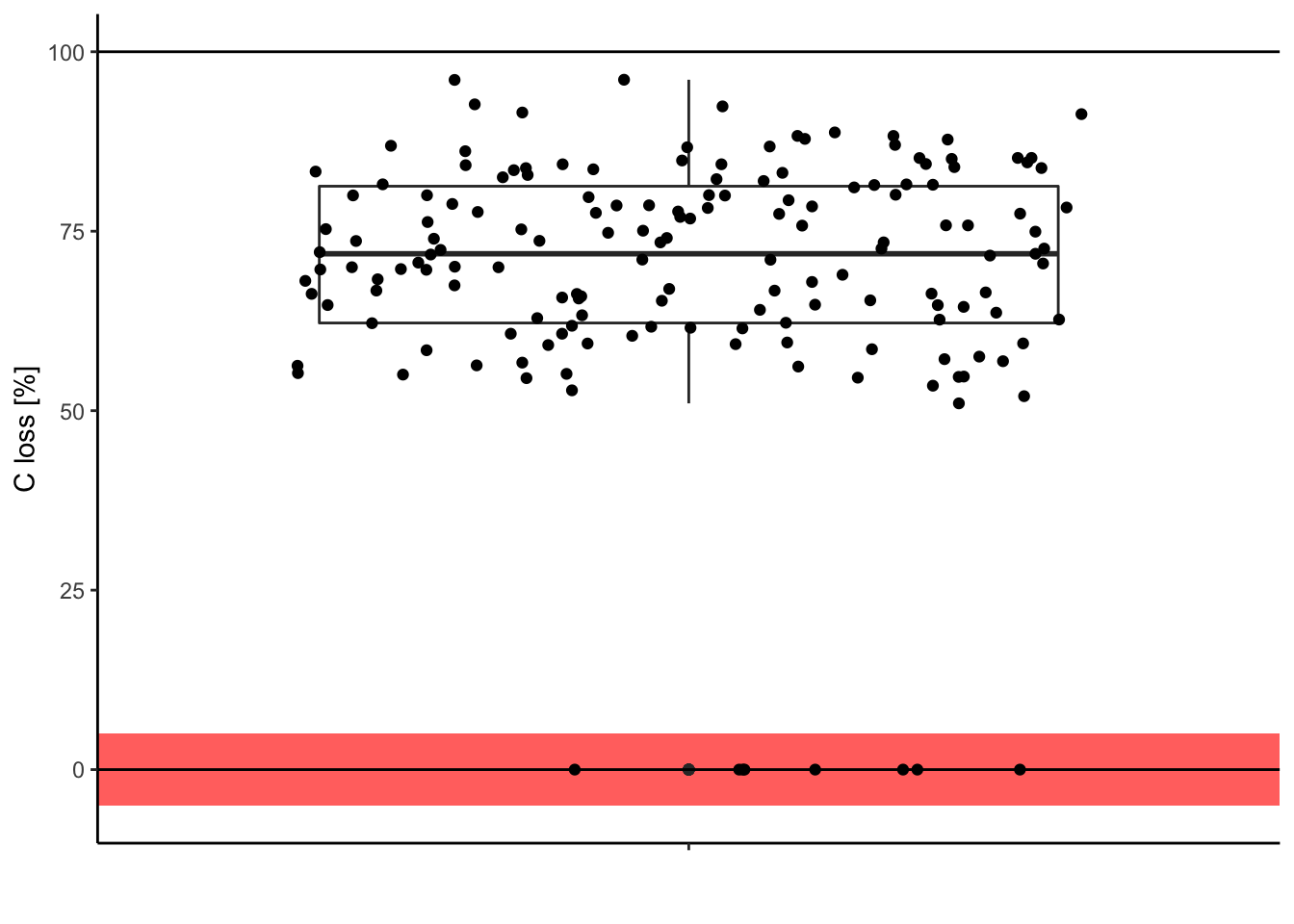

Is it meaningful to have 0% of carbon loss after one year of decomposition? In this case, it was only typos. So we can correct them in the original data.

Look at the relationship you are fitting

ggplot(data = df, aes(x = lit.rich, y = C.loss_Mi1)) + 
  geom_jitter() +  
  # all the regression line using a linear relationship (i.e. here the same that your model)
  geom_smooth(method = 'lm', color = 'black') +  
  labs(x = "Litter species richness", y = "C loss [%]") + 
  theme_classic()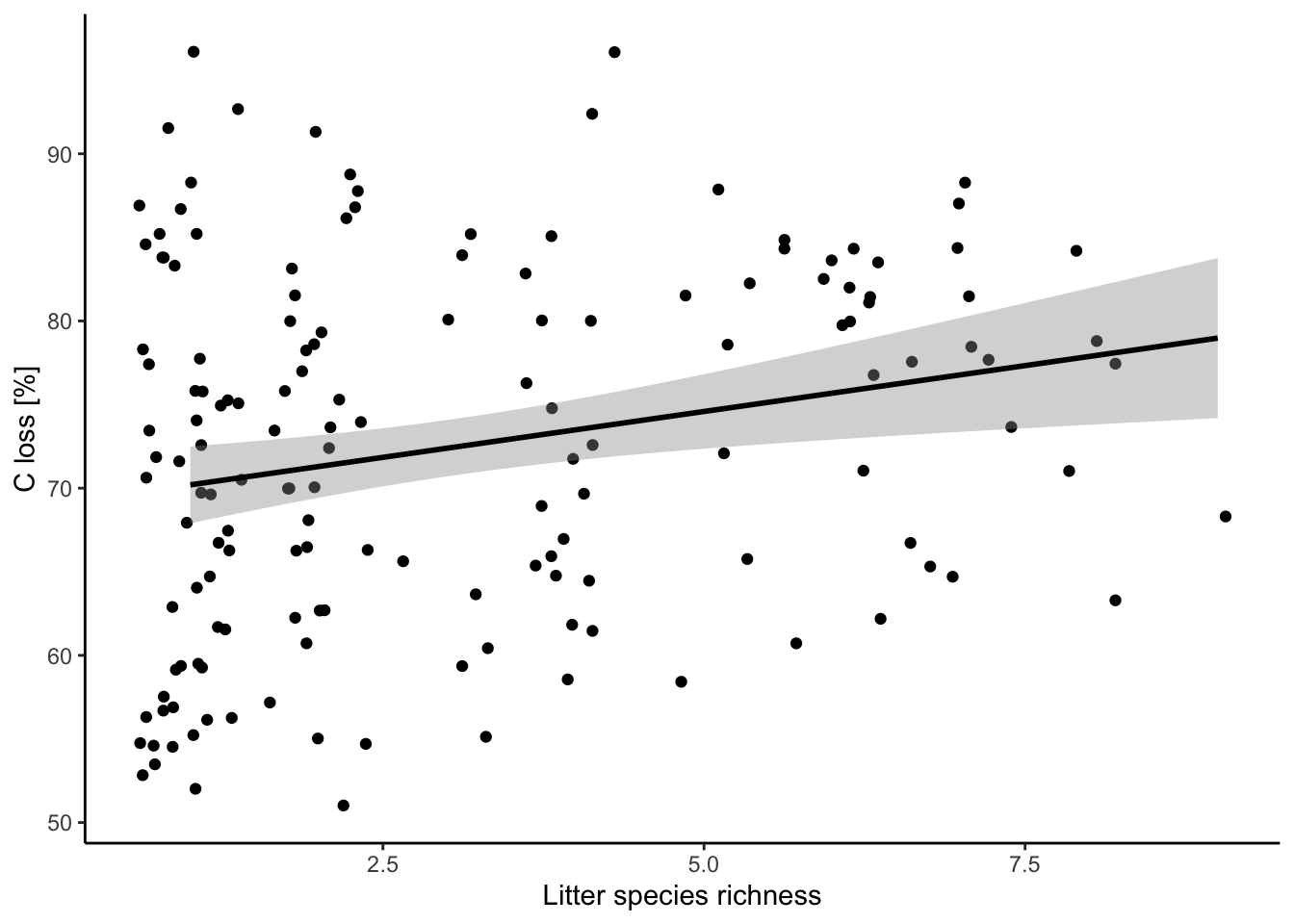

5.2. New model after corrections

mod = lm(data = df, formula = 'C.loss_Mi1 ~ lit.rich')
check_model(mod)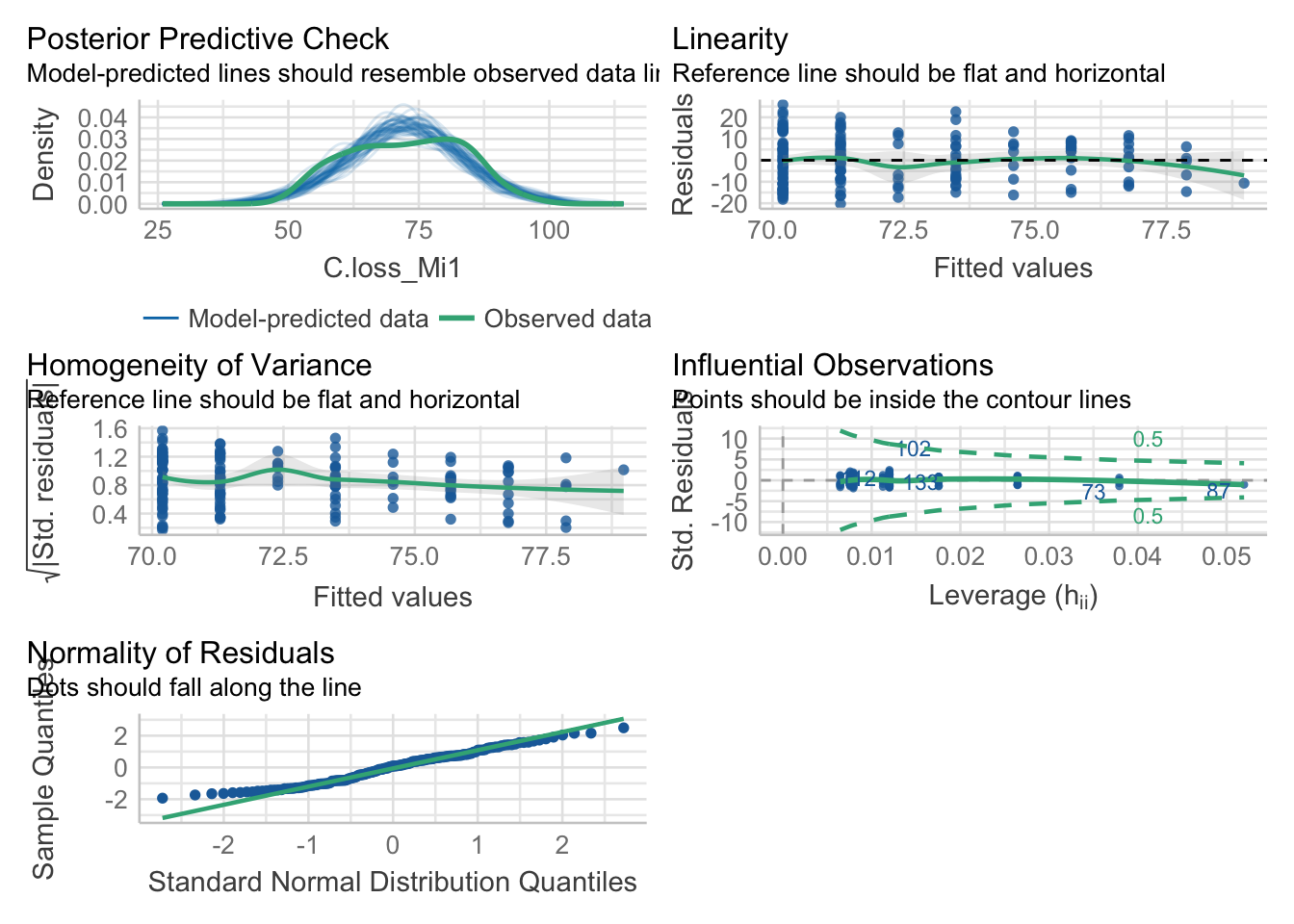

5.3. Data transformation

Log transformation of your explanatory variable.

ggplot(data = df, aes(x = lit.rich, y = C.loss_Mi1)) + 
  geom_jitter() +  
  # all the regression line using a linear relationship (i.e. here the same that your model)
  geom_smooth(method = 'lm', color = 'black') +  
  scale_x_continuous(trans = 'log', breaks = c(1,2,4,8)) + 
  labs(x = "Litter species richness", y = "C loss [%]") + 
  theme_classic()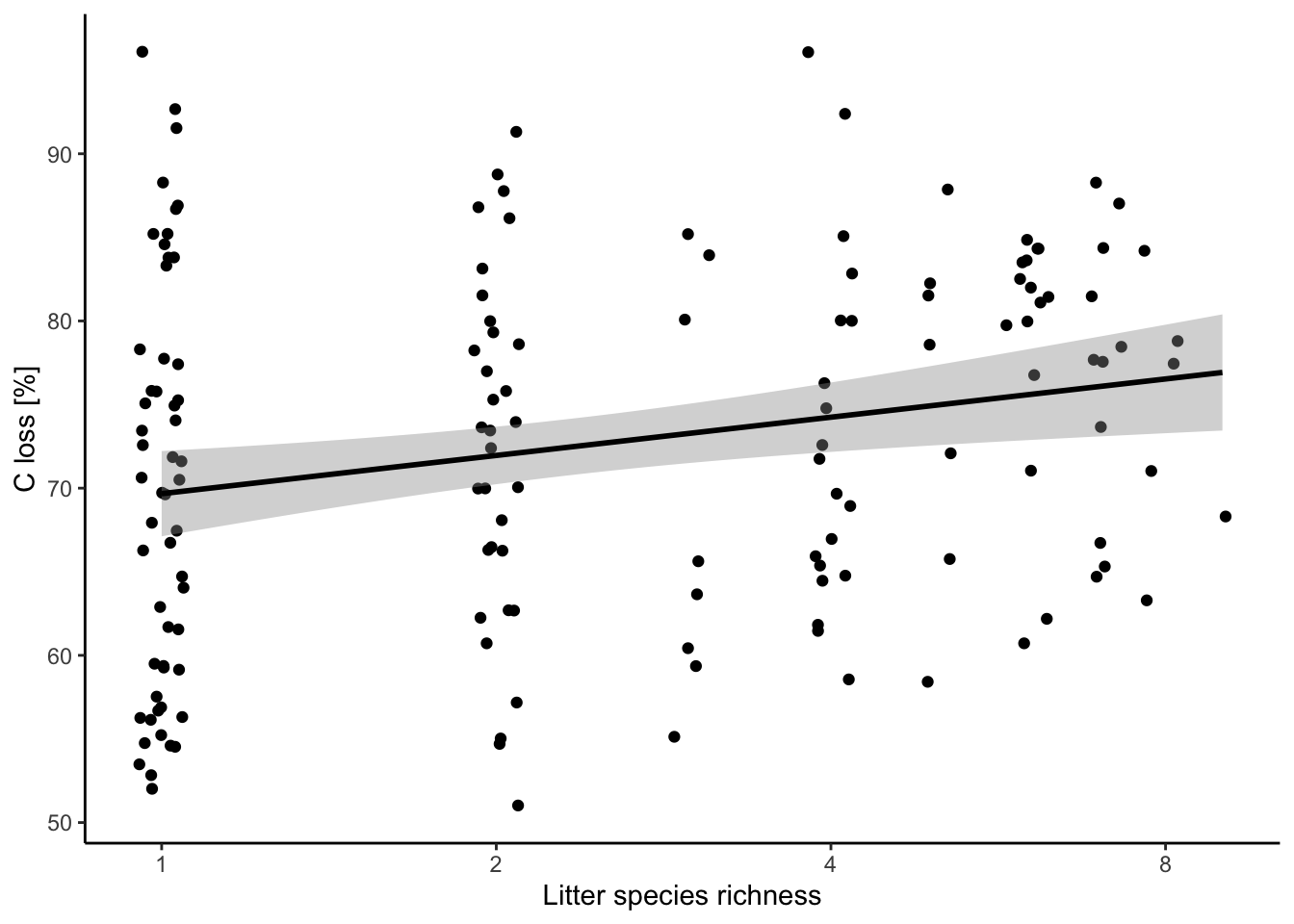

New model

mod.1 = lm(data = df, formula = 'C.loss_Mi1 ~ log(lit.rich)')

check_model(mod.1)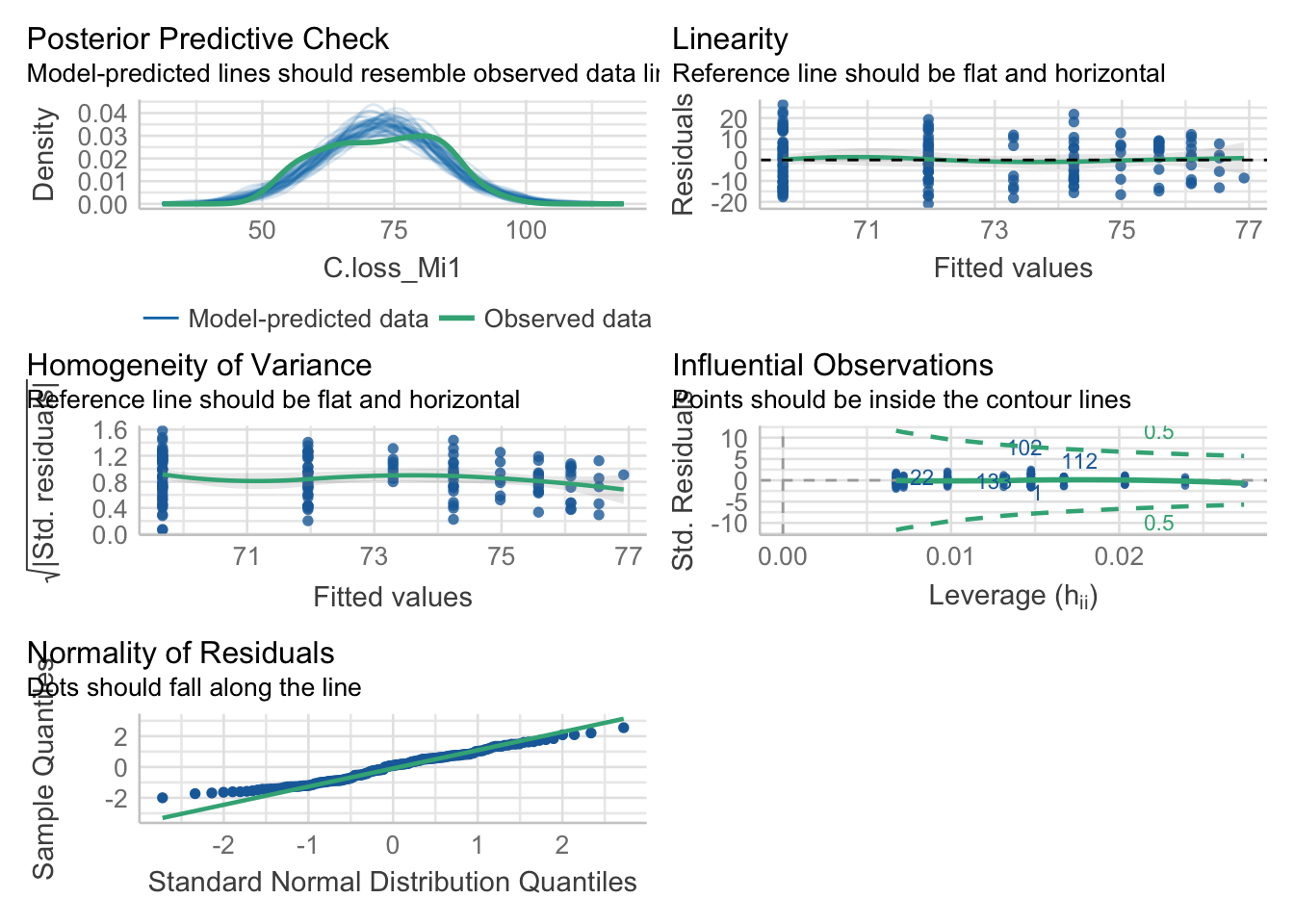

5.4. Compare the model quality

compare_performance(mod, mod.1)

## # Comparison of Model Performance Indices
## 
## Name  | Model |      AIC | AIC weights |      BIC | BIC weights |    R2 | R2 (adj.) |   RMSE |  Sigma
## -----------------------------------------------------------------------------------------------------
## mod   |    lm | 1176.469 |       0.484 | 1185.599 |       0.484 | 0.051 |     0.045 | 10.557 | 10.626
## mod.1 |    lm | 1176.338 |       0.516 | 1185.469 |       0.516 | 0.052 |     0.046 | 10.552 | 10.621

Data transformation doesn’t improve our model

6. Yes, extract your results

6.1. Check model summary

summary(mod)

## 
## Call:
## lm(formula = "C.loss_Mi1 ~ lit.rich", data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -20.2747  -8.7829   0.8984   7.5652  25.9039 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  69.1002     1.4516  47.602  < 2e-16 ***
## lit.rich      1.0972     0.3824   2.869  0.00469 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.63 on 153 degrees of freedom
## Multiple R-squared:  0.05107,    Adjusted R-squared:  0.04487 
## F-statistic: 8.234 on 1 and 153 DF,  p-value: 0.004693

6.2. Extract model coefficients

summary(mod)$coefficients

##              Estimate Std. Error   t value     Pr(>|t|)
## (Intercept) 69.100160  1.4516329 47.601675 1.272742e-93
## lit.rich     1.097198  0.3823676  2.869485 4.693330e-03

6.3. Extract model R squared

summary(mod)$r.squared

## [1] 0.05106831

6.4. Extract your fitted model

library(ggeffects)

predictions = ggpredict(model = mod, terms = 'lit.rich')

predictions

## # Predicted values of C.loss_Mi1
## 
## lit.rich | Predicted |         95% CI
## -------------------------------------
##        1 |     70.20 | [67.92, 72.48]
##        2 |     71.29 | [69.44, 73.15]
##        3 |     72.39 | [70.72, 74.07]
##        4 |     73.49 | [71.68, 75.30]
##        5 |     74.59 | [72.38, 76.80]
##        6 |     75.68 | [72.92, 78.44]
##        7 |     76.78 | [73.39, 80.17]
##        9 |     78.97 | [74.23, 83.72]

6.5 Plot your results

ggplot(data = df, aes(x = lit.rich, y = C.loss_Mi1)) +         # frame
  geom_jitter(data = df, aes(x = lit.rich, y = C.loss_Mi1)) +  # jitter add some noise in the x-axis to better show the points
  geom_line(data = predictions, aes(x = x, y = predicted)) +   # add the regression line, when you use different dataframes in the plot you need to define them for each geom
  labs(x = "Litter species richness", y = "C loss [%]") + 
  theme_classic()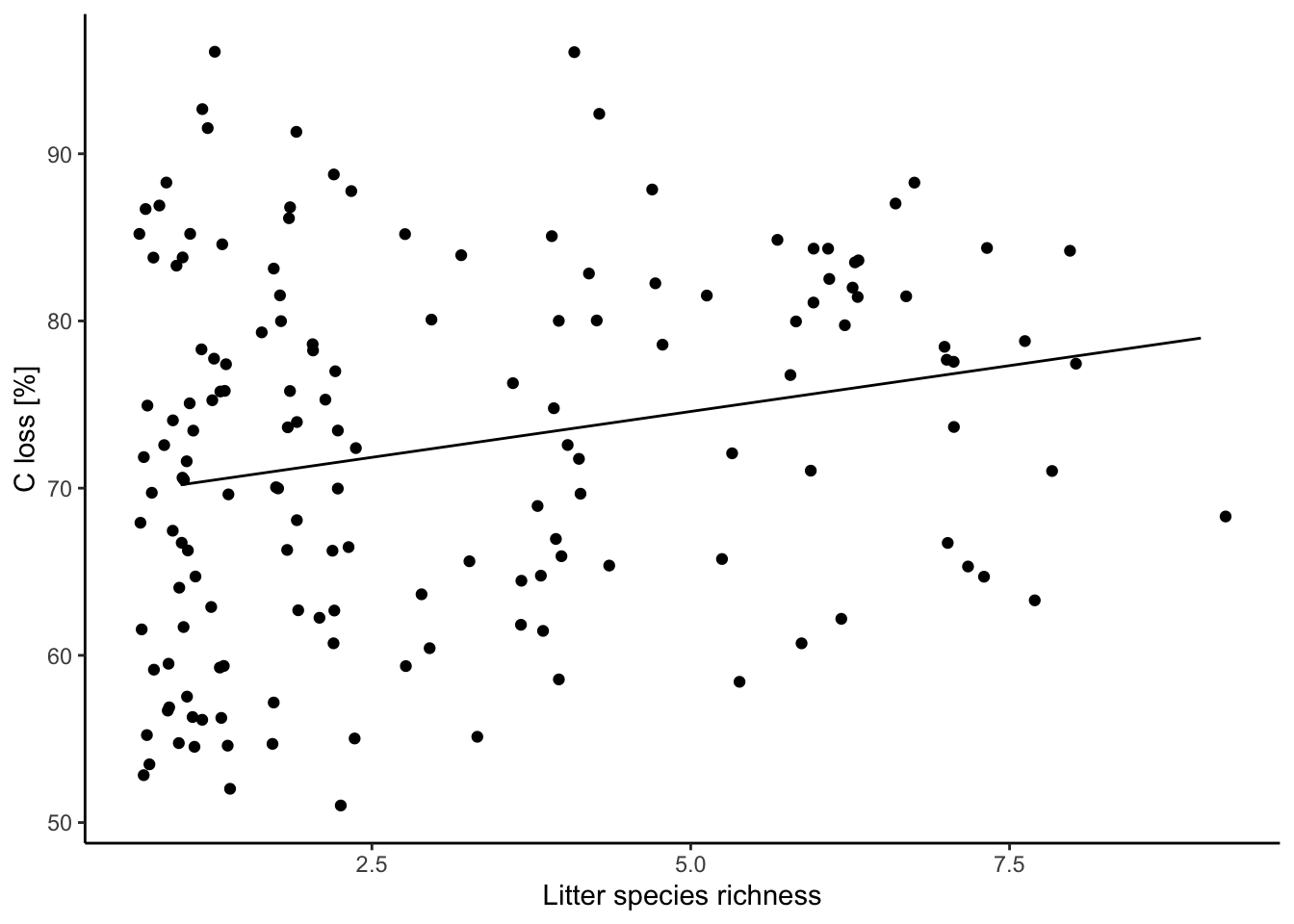

See ggplot packages for more details.

Useful links and tutorials

Google

The R bible: The R Book

Data handling

Tidyverse world:

The tidyverse packages:

loading Excel data with readxl

loading data with readr package

data handling with dplyr package

Building statistical model

Variable distributions (visual example)
Linear model with normally distributed residuals:
- ‘lm’ r documentation
- Tutorial
Linear model with other residuals distribution:
Non-linear models:
- by transforming your data: log, polynomial … tutorial
- by using the nls() function: tutorial
- (by building your own fitting and optimization functions and using a solver: tutorial)
General additive model: a great tutorial
Mixed effect models (using lm4):
- tutorial 1
- tutorial 2
- tutorial 3
- package vignette
- nice visualization to understand the process behind Mixed-effect models
Structural Equation Modeling:
- the Bible for SEM: Jon Lefcheck book
- tutorial
Spatio-temporal analyses with R:
- The Bible for Spatio-temporal modeling: book (pdf)
- Dealing with temporal auto-correlation in R: tutorial
A complete other world: Bayesian statistics:
- an introduction
- lecture using Stan
- paper

Model quality

The “performance” package

Plotting stuff

ggplot make your life easy and pretty
ggpubr an Add-On to ggplot2:
- package
- ggarrage to combine plots from ggplot

R tutorial stat

Introduction to stat in R: Cheatsheet

Content

Introduction

Stepwise analyses

1. Check your data

1.1. Load your data

1.2. Your dataset structure

1.3. Your data structure

1.3.1. Plot all the variables

1.3.2. Plot the variables’ distribution

1.3.3. Compare this distribution to the possible range of data

1.3.4. Clean your dataset

2. Build your hypotheses

2.1. Hypotheses

2.2. distribution

3. Build your model

3.1. Identify the parameters of your model

3.2. Fit your model on your data

4. Check your model fit. Are the statistical assumption met?

4.1. Model fit

4.2. Check outliers

4.3. Check possible distribution of residuals

4.4. Check normality of the residuals

4.5. Check heteroscedasticity of variance

5. No, data transformation and corrections

5.1. Check your data (again)

5.2. New model after corrections

5.3. Data transformation

5.4. Compare the model quality

6. Yes, extract your results

6.1. Check model summary

6.2. Extract model coefficients

6.3. Extract model R squared

6.4. Extract your fitted model

6.5 Plot your results

Useful links and tutorials

Data handling

Building statistical model

Model quality

Plotting stuff

Rémy Beugnon

Related